2016. 1. 10. 13:45ㆍ수학
1700년대에 d'Alembert에 의해 1차원 파동방정식의 일반해가 발견되었다. 그 과정을 하나씩 따라가보자.

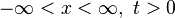
기본적으로 1차원 파동방정식이라함은 위와 같은 편미분방정식에 두 개의 초기조건(I.C., initial condition)을 더한 꼴을 의미한다.(이를 Cauchy problem이라고 한다)
우리는 달람버트의 방법대로, method of characteristics를 사용할 것이다.
먼저 변수를 치환하자.

x, t로 정리하면
각각 x, t로 편미분하면
연립해서 풀면

여기서 chain rule에 의해 다음의 사실을 알 수 있으므로
(1)을 이용해 파샬뮤와 파샬에타로 정리하면


따라서
이 된다.(이므로)
따라서 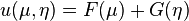 가 될 수 밖에 없고(
가 될 수 밖에 없고(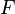 ,
,  는 적당히 좋은 함수) 치환했던 변수를 되돌리면
는 적당히 좋은 함수) 치환했던 변수를 되돌리면
 꼴이 된다.
꼴이 된다.
이제 초기조건을 이용해 일반해를 완성시킨다.
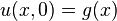 를 통해
를 통해  .
.
 를 통해
를 통해 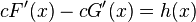 .를 쉽게 구할 수 있다.
.를 쉽게 구할 수 있다.
두 번째 식을 적분해 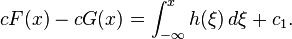 를 얻고
를 얻고
연립해 풀면
이걸  에 대입하면
에 대입하면
![u(x,t)={\frac {1}{2}}\left[g(x-ct)+g(x+ct)\right]+{\frac {1}{2c}}\int _{x-ct}^{x+ct}h(\xi )\,d\xi .](https://upload.wikimedia.org/math/7/4/a/74a2d794fd4c1f7aa5ef4de146b7d622.png)
를 얻고 이를 d'Alembert's formula라고 부른다.
재미있는 사실은 (x,t) 2차원상의 한 점(물리적으로 보면, 특정한 시각에 1차원 선의 특정한 한 점)의 파동의 크기 u는 오직 x-ct, x+ct 사이의 값에만 영향을 받는다는 점이다.
이를 물리학적으로 생각해보면 속도 c로 시간 t안에 도달할 수 있는 모든 점들이 저 점 x에 지금 영향을 끼치고 있다는 것인데(domain of dependence), 거꾸로 보면 무한히 긴 기타줄의 한 점x를 튕겼을 때 시간 t가 지난 뒤 그 튕김에 영향을 받는 범위는 x 플러스마이너스 ct 안의 모든 점이 될 것이다(range of influence).
이런 상식적인 현상도 파동방정식의 해를 통해 수학적으로 왜 그런지 알 수가 있다.
'수학' 카테고리의 다른 글
| 울프럼알파(wolfram alpha)로 사칙연산, 미적분, 라플라스 변환, 푸리에 변환 계산 (0) | 2016.01.07 |
|---|---|
| 리만 가설과 소수의 관계 (0) | 2016.01.06 |
| 소수에 관련된 증명되지 않은 주제들 (0) | 2016.01.05 |
| 실수집합의 완전성(completeness of real set) (0) | 2016.01.05 |
| 소수는 무한히 많다 (0) | 2016.01.05 |





