2016. 1. 6. 00:17ㆍ수학
리만 가설은 1859년 리만(Riemann)이 리만 제타 함수의 자명하지 않은 근(nontrivial zeros)들의 실수부가 1/2일 것이라고 추측한 곳에서부터 출발했다.
우선 리만 제타 함수(Riemann zrta function)가 무엇인지 살펴보자.
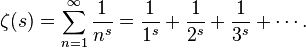
위와 같이 정의된 함수를 리만 제타 함수라 한다. 이 무한급수는 s가 1보다 클때에만 수렴해 정의가 되기 때문에, 언뜻 생각해선 이 급수가 0이 되는 s, 즉 리만 제타 함수의 근을 생각하기 어렵다. 하지만 리만은 이 제타 함수를 복소평면으로 확장시켜 s=1을 제외한 모든 복소평면에서 잘 정의되도록 만들었다. 저 급수는 s가 1보다 클 때의 제타 함수의 모습이라고 이해하면 쉽다. s가 1보다 작은 부분에 대해 제타 함수는 함수방정식으로 정의가된다. 실제로 제타 함수의 근은 -2, -4, -6,... 등 자명한 음의 정수들을 제외하면 모두 0과 1 사이에 분포한다.
이 제타 함수와 소수를 엮은 첫번째 인물은 역대급 천재 수학자 오일러였다.

위의 등식(identity)를 오일러곱(Euler Product)라 부르는데 증명은 다음과 같다.
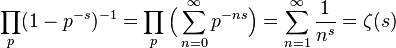
첫번째 등식은 수렴하는 기하급수(geometric series)의 성질을 이용하였고 두 번째 등식은 모든 소수와 소수의 n 제곱이 존재해 무한히 분배법칙을 사용하면 결국 모든 자연수를 얻을 수 있다는 성질을 이용했다.
하지만 이보다 강력한 제타 함수의 역할은 소수의 분포와 관련이 있다. 리만은 주어진 수 보다 작은 소수의 개수를 세는 소수 세기 함수(prime-counting function)
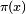 를 이용해 새로운 함수를 정의했다.
를 이용해 새로운 함수를 정의했다.

그 다음 이 새로운 소수 세기 함수를 아래의 함수를 이용해
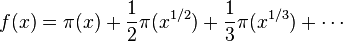
다음과 같이 표현해냈다.
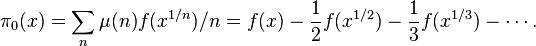
여기서 리만은 Riemann's explicit formula라고 불리는 아래의 등식을 발견해 내었는데,
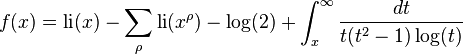
여기서 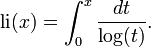 이고
이고 는 리만 제타 함수의 자명하지 않은 근(nontrivial zeros)을 뜻한다.
놀라운 점은 이 공식이 소수가 근사치에서 진동하는 진폭이 제타 함수의 실수부에 의해 컨트롤된다는 사실이다.
즉 리만 가설이 증명된다면 우리는 소수의 불규칙한 분포에 대해 한층 더 깊이 이해를 할 수 있게 된다고 할 수 있겠다.
'수학' 카테고리의 다른 글
| 1차원 파동방정식의 해, d'Alembert's formula (0) | 2016.01.10 |
|---|---|
| 울프럼알파(wolfram alpha)로 사칙연산, 미적분, 라플라스 변환, 푸리에 변환 계산 (0) | 2016.01.07 |
| 소수에 관련된 증명되지 않은 주제들 (0) | 2016.01.05 |
| 실수집합의 완전성(completeness of real set) (0) | 2016.01.05 |
| 소수는 무한히 많다 (0) | 2016.01.05 |